What happens to latency if service time is cut in half
Introduction
The goal of this post is to determine how the latency is going to be impacted if the service time is going to be cut in half. I was watching a great presentation of Martin Thompson where he mentioned this example example and wanted to freshen up my queuing theory a bit and do some calculations.
Lots of formulas
Let’s first get some formulas out of the way.
The mean latency as function of the utilization:
\[R=\dfrac{1}{\mu(1-\rho)}\]- \(R\) is latency (residency time)
- \(\mu\) is service rate
- \(\rho\) is utilization
\(\mu\) is the reciprocal of service time \(S\).
\[\mu=\dfrac{1}{S}\]And if we fill this in and simplify the formula a bit, we get the following:
\[R=\dfrac{1}{\dfrac{1}{S}(1-\rho)}\] \[R=\dfrac{S}{(1-\rho)}\]Another part we need is the calculation of the utilization:
\[\rho = S \lambda\]- \(\rho\) is the utilization
- \(\lambda\) is the arrival rate.
- \(S\) is the service time.
This formula is known as the Utilization Law or Little’s Microscopic Law.
And this can be converted into a function that calculates the arrival rate as a function of utilization and service time:
\[\lambda = \dfrac{S}{\rho}\]Comparing the latencies
In Martin’s example he has 2 services:
- an unoptimized service with \(S=0.1\) seconds.
- an optimized service with \(S=0.05\) seconds
To make it a bit more tangible let’s plot latency curves as function of utilization for both services.
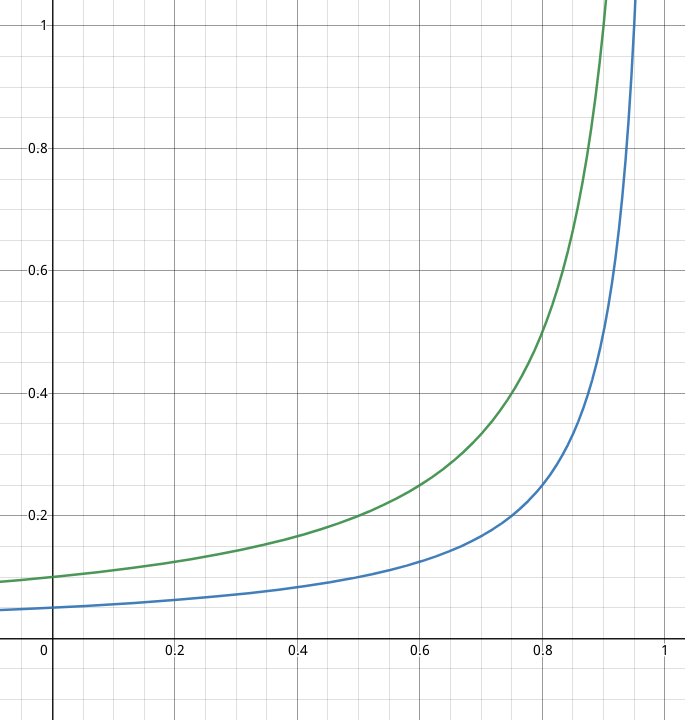
- green: unoptimized service
- blue: optimized service
The x-axis is the utilization and the y-axis is the latency.
The first thing we can calculate is the latency with a service time of 0.10 seconds and a utilization of 0.90 because this utilization Martin picked in his example:
\(R=\dfrac{S}{(1-\rho)}=\dfrac{0.10}{(1.0-0.90)}=1.0\) second.
The next part we need to determine is the arrival rate based on the utilization and service time. So with a service time of 0.10 and a utilization of 0.90 we get the following arrival rate:
\(\lambda = \dfrac{S}{\rho} = \dfrac{0.1}{1-0.9} = 10\) requests/second.
So if the service time is going to be cut in half, and we keep the same arrival rate, the utilization is going to be cut in half:
\[\rho = S \lambda = 0.05 \times 10 = 0.45\]And if fill this into the calculate the latency is function of the utilization for the optimized service, we get:
\(R=\dfrac{S}{(1-\rho)} = \dfrac{0.05}{1-0.45}=0.091\) seconds.
We can see both the calculated latencies in the plot below:
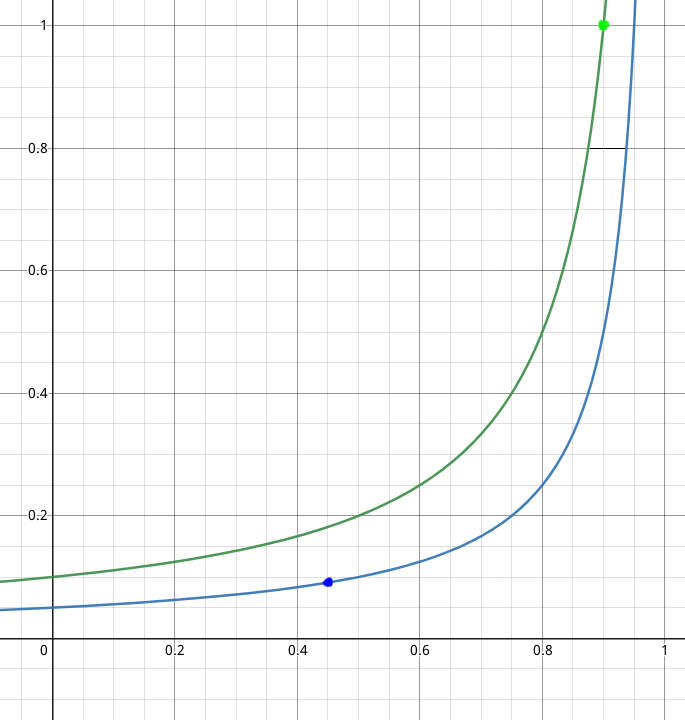
So we went from a latency of 1 second to 0.091 seconds which is an \(\dfrac{1}{0.091}=11\) times improvement.
Discrepancy
Martin’s claim is that the latency improvement is 20x. But the results based on the above formulas don’t agree with that. He makes a remark that the unit of processing is half the calculated latency, but I don’t understand what he means or how this is relevant for the latency calculation.
I haven’t configured comments yet on this new website. So if you want to comment, send me a message on Twitter.